卡尔曼滤波(Kalman filter)

测量值

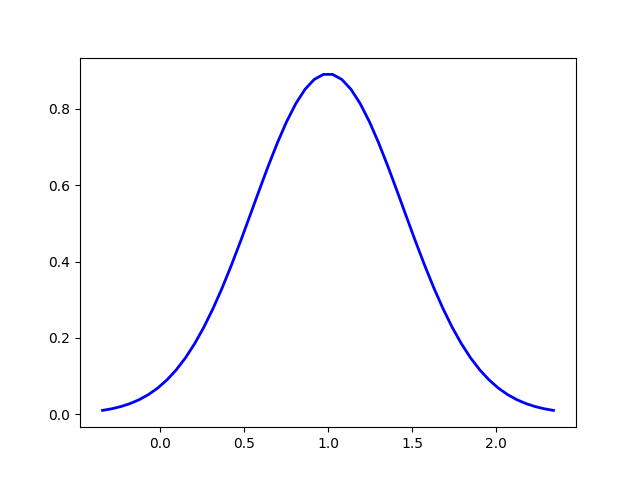
在讲卡尔曼滤波之前，我觉得必须强调的一件事就是对于测量值的理解。举个例子，比如我们测得桌子的长度是1米。我们知道误差肯定是存在的，所以这个桌子的长度可能实际上是1.01米或者0.99米。所以桌子的长度的测量值是1米，其实可以理解成桌子的长度是1米的概率最大。如果我们认为桌子的长度满足正态分布，我们也就会发现这个1米其实就是正态分布的均值，因为正态分布均值出现的概率是最高的。从概率分布函数上可以看出，桌子长度也可能是其他值，但是概率比1米要小。

思路

对于卡尔曼滤波的入门理解，我觉得还是先抛开矩阵会好一些。矩阵对于表示公式，参与计算等十分方便。但是如果你连整个算法的框架与思路都不了解，矩阵表示只会给你学习带来更大的难度。也许你记住了所有矩阵表示，但是你会发现，真正实际应用时，你会一脸懵，无从下手。边实践边学习边理解是高效的学习方法。

其实卡尔曼滤波的思路很简单，但于需要根据不同场景具体分析。它的思路其实就是根据多传感器有交集的特点，进行数据融合。什么是有交集呢？简单来讲就是你的一个信息，可以通过一个传感器直接读出，或者可以多个传感器运算得出。举个例子就是，对于你当前的位置，你可以通过GPS获得，你也可以通过你1小时前的位置结合你1小时走过的路程获得。前者就是卡尔曼滤波中的测量值，后者则是卡尔曼滤波中的预测值。

测量值我们是可以直接获得的，预测值我们是需要通过不同场景去分析的。

高斯融合分布

那么问题来了，我们有了这个预测值和测量值，这两个值我们要怎么应用，才能找到最优值呢。

还是同一个思路，这里的两个值，其实都是两个高斯分布，对应着两个均值和两个方差。测量的方差需要采样获得，预测的方差根据调试给出。因为自回归的原因，预测方差影响的是收敛速度。我们现在要把这两个高斯分布进行运算获得最优解。

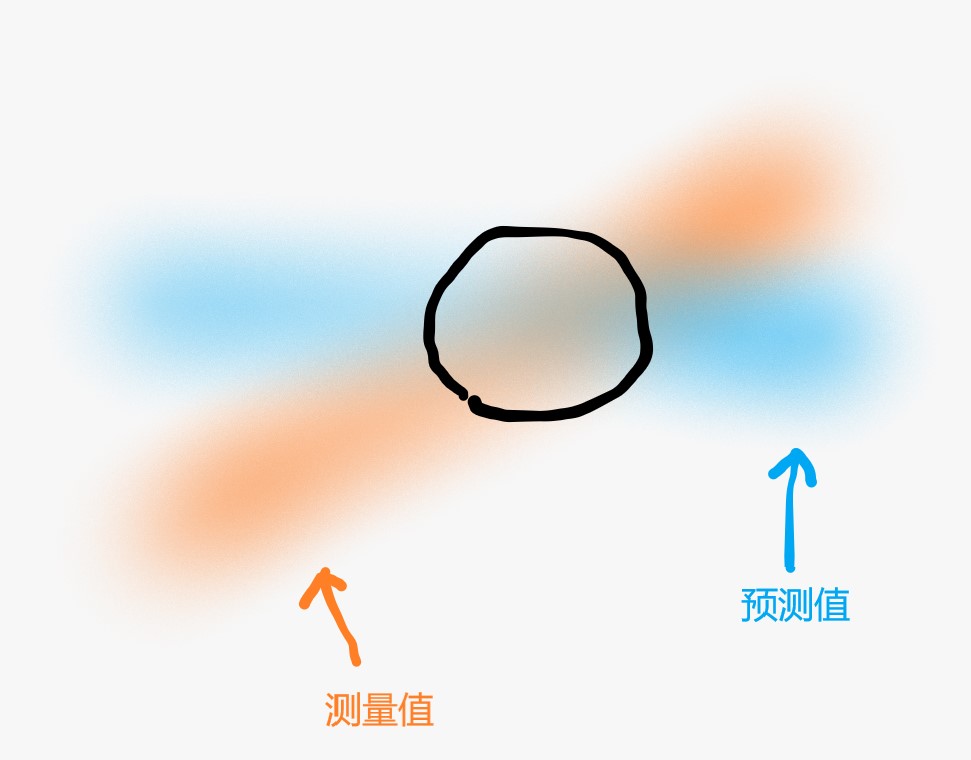
看下面这个图，橙色区域代表测量值，蓝色区域代表预测值。其实实际上整副图像都有测量值和预测值，只是没有颜色的区域的概率很小，有颜色的区域可以理解成3$\sigma$​​​​​​​​​​​​​区域内。很明显看出，我们需要的最优解就是画圈的地方，也就是测量值和预测值的交集，我们需要将两个高斯分布融合，也就是相乘。

（高斯融合有详细的化简过程，嫌复杂的也可以直接看结果）

假设有两个高斯分布 测量值代表的高斯分布均值为$\mu_1$​​​，方差为$\sigma_1$​​​，预测值代表的高斯分布均值为$\mu_2$​​​，方差为$\sigma_2$​​。

则两个高斯分布的概率分布如下

$$f(x) =\frac{1}{\sqrt{2\pi}\sigma_1}e^{-\frac{(x-\mu_1)^2}{2\sigma_1^2} }$$

$$g(x) =\frac{1}{\sqrt{2\pi}\sigma_2}e^{-\frac{(x-\mu_2)^2}{2\sigma_2^2} }$$

将两个概率分布相乘

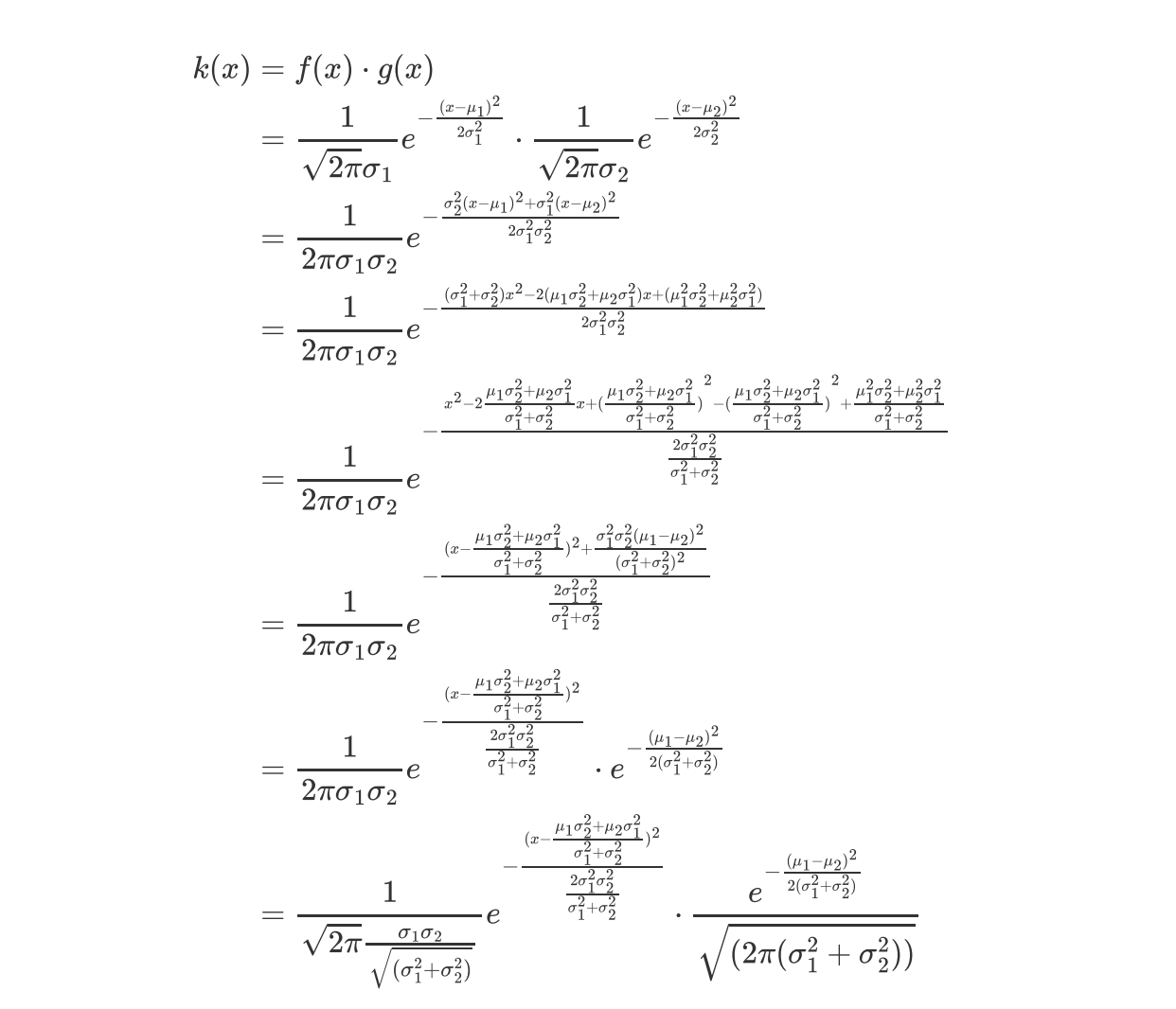
（当前只支持行间和行内公式渲染 所以就采用图片的方式）

所以结果是一个均值$\mu_0$​​=$\frac{\mu_1\sigma_2^2+\mu_2\sigma_1^2}{\sigma_1^2+\sigma_2^2}$​​，方差$\sigma_0$​​=$\frac{\sigma_1\sigma_2}{\sqrt{\sigma_1^2+\sigma_2^2}}$​​的高斯分布乘以一个系数$k_0$​​=$\frac{e^{-\frac{(\mu_1-\mu_2)^2}{2(\sigma_1^2+\sigma_2^2)}}} {\sqrt{(2\pi(\sigma_1^2+\sigma_2^2))}}$​​。

将结果归一化，使得总概率为1，也就是去掉这个系数$k_0$​​​​​。

对于结果这个高斯分布，我们也是需要取概率最大的值，也就是均值。所以这里的$\mu_0$​​​也就是我们需要的最优解。

至于大家经常见到的卡尔曼增益其实就是$gain =\frac{ {\sigma_2}^2}{ {\sigma_1}^2+{\sigma_2}^2}$​​​。

最优解的另一种表示方式是$best =\mu_2 + gain*(\mu_1-\mu_2)$​​​。其实化简一下也就是上述的$\mu_0$​。

计算出最优值后，需要进行自回归，需要用到这里的$\sigma_0$​​。我们称为当前值距离最优值的方差。

其实如果完全带入公式的话，应该也不会出现卡尔曼增益。但是其实$\mu_0$和$\sigma_0$​的计算有重复的地方，个人觉得卡尔曼增益的意义就是更好地表示和计算，也可能是对其了解得还不够深。

具体例子

以雷达的一束数据为例，结合全场定位的数据，运用卡尔曼滤波获得当期最优解。

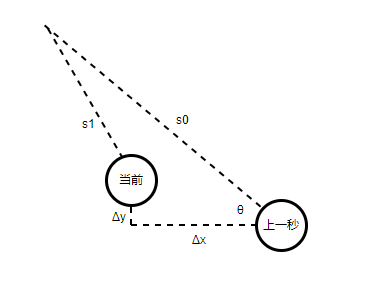
假设全场定位上一秒的数据为$x_0$和$y_0$，当前的数据为$x_1$和$y_1$​，

则车子在这一秒运动的$\Delta x=x_1-x_0$，$\Delta y=y_1-y_0$。

假设雷达上一秒的数据为$s_0$​​，则可以预测当前的雷达数据为$s'=\sqrt{(s_0\cos{\theta}-\Delta x)^2+(s_0\sin{\theta}-\Delta y)^2}$​。

而当期测得的雷达数据是$s_1$，我们要把$s'$和$s_1$进行融合。

我们先设定当前值距离最优值的方差为$\sigma$，这个值会随着自回归而收敛，不要为0即可。

假设我们给定预测方差为$\sigma_0$​​，则我们预测的雷达的方差$\sigma'=\sqrt{\sigma^2+\sigma_0^2}$​​​。​

假设我们测量方差为$\sigma_1$。我们现在相当于拥有两个正态分布

测量：均值$s_1$​​，方差$\sigma_1$​​，预测：均值$s'$​​，方差$\sigma'$。

ok，那我们要的最优解$best=\frac{s_1\sigma'^2+s'\sigma_1^2}{\sigma_1^2+\sigma'^2}$，然后自回归，$\sigma=\frac{\sigma_1\sigma'}{\sqrt{\sigma_1^2+\sigma'^2}}$​。

当然这里用卡尔曼增益可以减少重复计算量，即

$gain =\frac{ {\sigma_1}^2}{ {\sigma_1}^2+{\sigma'}^2}$​​，$best =s' + gain*(s_1-s')$​​，$\sigma=\sqrt{(1-gain)*\sigma'^2}$​​​。

完成√

参考

reference:https://www.zhihu.com/question/23971601/answer/770830003

reference:https://blog.csdn.net/u010720661/article/details/63253509

reference:https://blog.csdn.net/Ronnie_Hu/article/details/111378283