7dof_robot

这学期机器人学的大作业是做一个七自由度机械臂，

其中六个转动关节，一个伸缩关节

前三个转动关节+一个伸缩关节+末尾三个转动关节

这里记录一下我耗时最久的解析解

首先其实七自由度是有冗余的，我们求解只需要求解六个关节，

我是求解六个旋转关节，然后伸缩关节用于后续规划。

这种解析解的方法是适用于常规机械臂，即前面的关节确定腕部位置，后三个关节确定姿态。

求解$\theta_1$ $\theta_2$ $\theta_3$

将机械臂简化成下图，用于分析解析解。

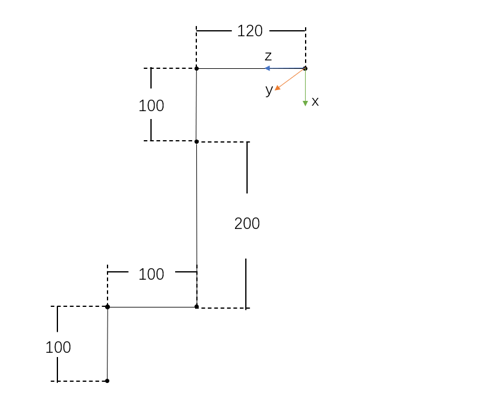
我们已知机械臂末端的位姿$^{0}T_7$

$$^{0}T_7 = ^0T_1\, ^1T_2\, ^2T_3\, ^3T_4\, ^4T_5\, ^5T_6\, ^6T_7 = \begin{bmatrix} ^{0}R_7 & ^{0}P_7 \\ 0 & 1\\ \end{bmatrix}$$

首先我们根据末端坐标系将$P_{07}$转换到$P_{06}$，记$a$为${^{0}}R_7.a$，则

$$^{0}P_6 = {^{0}}P_7 - aL$$

而坐标系5与坐标系6原点重合，所以有

$$^{0}P_5 = {^{0}}P_6$$

现在已知$^{0}P_5$，而$^{0}P_5$仅是关于$\theta_1$，$\theta_2$，$\theta_3$的函数。三个未知数，三个方程，可解。将其不断展开如下

$$\begin{matrix} ^{0}P_5 = {^{0}}T_1 \, ^{1}T_2 \, ^{2}T_3 \, ^{3}T_4 \, ^{4}P_5 \\ \end{matrix}$$

$$= {^{0}}T_1 \, ^{1}T_2 \, ^{2}T_3 \, ^{3}T_4 \, \begin{bmatrix} 0 \\ 0 \\ d_5 \\ 1 \\ \end{bmatrix}$$

$$={^{0}}T_1 \, ^{1}T_2 \, ^{2}T_3 \, \begin{bmatrix} 0 \\ 0 \\ d_4+d_5 \\ 1 \\ \end{bmatrix}$$

$$= {^{0}}T_1 \, ^{1}T_2 \, \begin{bmatrix} (d_4+d_5)S\theta_3 \\ -(d_4+d_5)C\theta_3 \\ 0 \\ 1 \\ \end{bmatrix}$$

$$= {^{0}}T_1 \, \begin{bmatrix} f_1C\theta_2-f_2S\theta_2+a_2C\theta_2 \\ f_1S\theta_2+f_2C\theta_2+a_2S\theta_2 \\ f_3 \\ 1 \\ \end{bmatrix}$$

$$= \begin{bmatrix} g_1C\theta_1+g_3S\theta_1 \\ g_1S\theta_1-g_3C\theta_1 \\ g_2+d_1 \\ 1 \\ \end{bmatrix}$$

其中

$$f_1 = (d_4+d_5)S\theta_3 \quad\qquad g_1 = f_1C\theta_2-f_2S\theta_2+a_2C\theta_2\\ f_2 = -(d_4+d_5)C\theta_3 \qquad g_2 = f_1S\theta_2+f_2C\theta_2+a_2S\theta_2\\ f_3 = 0 \qquad\qquad\qquad\qquad g_3 = f_3\\$$

所以

$$\begin{bmatrix} p_x-aL \\ p_y-aL \\ p_z-aL \\ \end{bmatrix} = \begin{bmatrix} g_1C\theta_1+g_3S\theta_1 \\ g_1S\theta_1-g_3C\theta_1 \\ g_2+d_1 \\ \end{bmatrix}$$

通过平方和可以消掉$\theta_1$，令

$$r = ({p_x-aL})^2 + ({p_y-aL})^2 + ({p_z-aL})^2 = k_1(\theta_2,\theta_3)$$

且

$$p_z - aL = g_2+d_1 = k_2(\theta_2,\theta_3)$$

则我们获得了两个仅含未知数$\theta_2$和$\theta_3$的两个方程，可解。化简可得

$$\theta_3 =asin[\frac{r-(d_4+d_5)^2-{a_2}^2+{d_1}^2-2 d_1 z}{2 a_2 (d_4+d_5)}]$$

观察得$g_3=0$，所以

$$\theta_1 =atan2(p_y-aL,p_x-aL)$$

求解$\theta_2$是求解

$$AC\theta_2 + BS\theta_2 = C$$

其中

$$A = -(d_4+d_5) C\theta_3 \\ B = a_2+(d_4+d_5) S\theta_3 \\ C = z -d_1 \\$$

设

$$t = tan\frac{\theta_2}{2}$$

则

$$cos(\theta_2)=\frac{1-t^2}{1+t^2} \\ sin(\theta_2)=\frac{2t}{1+t^2} \\$$

所以可解得

$$t = \frac{B \pm \sqrt{B^2+A^2-C^2}}{A+C} \\ \theta_2 = 2atan(t) \\$$

假设$\theta_1,\theta_2,\theta_3$的取值范围为$(0 \sim 2\pi)$，

则$\theta_1,\theta_2,\theta_3$各有两个解，共八组解，但是其中有四组解是错误的。

原因在于求解$\theta_1$时使用$\theta_1 =atan2(y,x)$，只关注$y$和$x$的比值关系，

有四组错误的解是$y$和$x$与正确的解正负号颠倒，

故我们要增加一个关于$x$或者关于$y$的条件，

在八组解里筛选出来正确的解。可以使用条件如下

$$\begin{matrix} p_x-aL = g_1C\theta_1+g_3S\theta_1 \\ p_y-aL = g_1S\theta_1-g_3C\theta_1 \\ \end{matrix}$$

最终可解得正确的四组$\theta_1,\theta_2,\theta_3$。

四组解其实只对应两种姿态，同姿态的两组解$\theta_3$相差$\pi$

对于三角函数的解的特殊情况，做如下处理

如果不在工作空间的点，$\theta_3$求解为复数，则不继续计算。

求解$\theta_2$有可能出现单解情况，处理成两个相同的解，保证最后有四组解。

求解$\theta_5$ $\theta_6$ $\theta_7$

已知$\theta_1,\theta_2,\theta_3$，可得到$^{0}T_3$

$$\begin{matrix} ^{0}T_3 = {^{0}}T_1 \, ^{1}T_2 \, ^{2}T_3 \\ \end{matrix}$$

又已知$^{0}T_7$，所以可得$^{3}T_7$

$$\begin{matrix} ^{3}T_7 = ^{3}T_0 \, ^{0}T_7 \\ \end{matrix}$$

因为

$$^{3}R_7 = \begin{bmatrix} S\theta_5 S\theta_7 + C\theta_5 C\theta_6 C\theta_7 & C\theta_7 S\theta_5-C\theta_5 C\theta_6 S\theta_7 & C\theta_5 S\theta_6 \\ -C\theta_5 S\theta_7 + S\theta_5 C\theta_6 C\theta_7 & -C\theta_7 C\theta_5-S\theta_5 C\theta_6 S\theta_7 & S\theta_5 S\theta_6 \\ C\theta_7 S\theta_6 & -S\theta_6 S\theta_7 & -C\theta_6 \\ \end{bmatrix}$$

所以，当$S\theta_6 \neq 0$时，

$$\begin{matrix} \theta_6 = atan2(S\theta_6, C\theta_6)\\ \theta_5 = atan2(R_{23}, R_{13})\\ \theta_7 = atan2(-R_{32}, R_{31})\\ \end{matrix}$$

当$S\theta_6 = 0$时，

$$\theta_6 = \pi , \theta_5=0 , \theta_7=atan2(R_{12}, -R_{11})\\ \theta_6 = 0 , \theta_5=0 , \theta_7=atan2(-R_{12}, R_{11})$$

所以最终我们可以解得四组$\theta_1,\theta_2,\theta_3,\theta_5,\theta_6,\theta_7$。

确定最后的解

因为没有实际躲避碰撞要求，规划最后解就采用关节变化最小的解。

内循环则挑选四组解中与当前关节角度变化最小的一组解

外循环则迭代伸缩关节，计算出不同伸缩关节长度对应的关节变化的最小值的解

然后最后再取所有的最小值，即为最后的解。

Matlab代码

其中全局的Link包含了机械臂的各种当前信息

解析解求解完也只需更新Link

function analytical_inverse_slove(T,dz,dx,alf,telescopic_length)
% 逆运动学求解 解析解 然后更新到目前Link的角度
% T为末端位姿
% dz dx alf为DH表参数
% telescopic_length可伸缩的长度
 			
 			
    % 获得当前关节角度 用于做解的判断
    global Link
    theta = zeros(1,7);
    for i = 2:8
        theta(i-1) = Link(i).th;
    end
 			
 	% 根据伸缩关节dh表的正负确定迭代的最小值和最大值
    if dz(4)<0
        dz_min = dz(4) - telescopic_length;
        dz_max = dz(4);
    else
        dz_min = dz(4);
        dz_max = dz(4) + telescopic_length;
    end
 			
    % 伸缩关节规划
    ths = []; % 存放关节伸缩规划过程中可用的th
    dzs = []; % 存放关节伸缩规划过程中对应的伸缩关节长度
 	for m = dz_min:2:dz_max     
 		dz(4) = m ;
 			
        link_target = T(1:3,4) + T(1:3,3) * abs(dz(7)); % 末端到最后一个关节
        r = sum(link_target.*link_target); % x^2+y^2+z^2
        x = link_target(1);
        y = link_target(2);
        z = link_target(3);
 			
 		% 求解th3
        th3_1 = asin((r-(dz(4)+dz(5))^2-dx(2)^2+dz(1)^2-2*dz(1)*z)/(2*dx(2)*(dz(4)+dz(5))));
        th3_2 = pi-th3_1;
        th3 = [th3_1,th3_2];
 			
        % 求解th1
        th1_1 =atan2(y,x);
        th1_2 = th1_1 + pi;
        th1 = [th1_1,th1_2];
 			
 		% 求解th2    
 		th_123 = zeros(4,3); % 四个解
 		index =1;
 		for j =1:length(th1)
 			for i=1:length(th3)   
                A = -(dz(4)+dz(5))*cos(th3(i));
                B = dx(2)+(dz(4)+dz(5))*sin(th3(i));
                C = z -dz(1);
                th2_1_2=solve_cos_plus_sin(A,B,C); % 两个解
 				for k=1:length(th2_1_2)
 					g1 = (dx(2)+(dz(4)+dz(5))*sin(th3(i)))*cos(th2_1_2(k))+...
 						 (dz(4)+dz(5))*cos(th3(i))*sin(th2_1_2(k));
 					if abs(cos(th1(j))* g1-x)<1e-11 && abs(sin(th1(j))* g1-y)<1e-11
 						th_123(index,:) = [th1(j),th2_1_2(k),th3(i)];
 						index = index + 1;
 					end
 				end
 			end
 		end
 			
 		if ~isreal(th_123) 
 			continue  %无解则保留之前的角度
 		end
 		
 		% 求解th5 th6 th7 			
        R06 = T(1:3,1:3);
        th_567 = ones(size(th_123,1),3);
        for i = 1:size(th_123,1)
            T01 = getT(th_123(i,1),dz(1),dx(1),alf(1));
            T12 = getT(th_123(i,2),dz(2),dx(2),alf(2));
            T23 = getT(th_123(i,3),dz(3),dx(3),alf(3));
            T03 = T01 * T12 * T23;
            R03 = T03(1:3,1:3);
            R36 = R03 \ R06;
 			[th_567(i,1), th_567(i,2), th_567(i,3)] = solve_R36(R36);    
 		end
 			
 		th = [th_123, zeros(size(th_123,1),1), th_567]; %4行7列
 			
 		errs = zeros(1,4);
 		for i = 1:size(th_123,1)
 			errs(i) = sum((th(i,:) - theta) .* (th(i,:) - theta));
 		end
 		[~,min_index]=min(errs);			
 			
 		ths = [ths;th(min_index,:)];
 		dzs = [dzs;m];
 	end
 			
 	if size(ths,1)~=0
 		errs = zeros(1,size(ths,1));
 		for i = 1:size(size(ths,1))
 			errs(i) = sum((ths(i,:) - theta) .* (ths(i,:) - theta));
 		end
 		[~,min_index] = min(errs); %关节变化最小
 			
 		dz(4) = dzs(min_index);
 		calc_DH(ths(min_index,:),dz,dx,alf); %更新到Link
 	end
 			
end

参考：https://www.bilibili.com/video/BV1v4411H7ez?p=30